En 1895, a los diecisiete años, Albert Einstein se planteó la siguiente paradoja: ¿qué sucedería si persiguiera un rayo de luz? Esta paradoja, que le persiguió durante diez años, le llevó a formular una de sus principales teorías: la Relatividad Especial. Esta cambió por completo el pensamiento de la época, y dio las primeras pistas de la teoría que más tarde le haría famoso.
Esta teoría fue formulada por primera vez en 1905, en un artículo que llevaba el título de "Sobre la electrodinámica de los cuerpos en movimiento" . Este artículo de treinta y un páginas, que revolucionaría la Física, se basaba en dos simples postulados:
-Las leyes físicas adoptan la misma forma en todo sistema de referencia que se considere en movimiento uniforme (principio de la relatividad).
-La velocidad de la luz en el vacío es la misma para cualquier sistema de referencia inercial (invariancia de c).
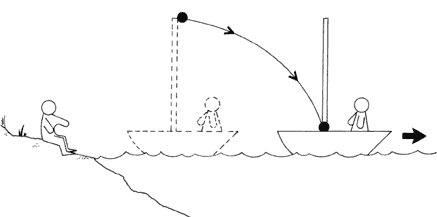
Vamos a explicar ambos postulados. Para explicar el primero es útil el siguiente ejemplo. Imagine que usted lanza una piedra a un barco. Para medir el movimiento de la piedra necesita basarse en un "sistema" o lugar y momento del movimiento. Ahora bien, ¿debería medirlo con respecto al barco o con respecto a la Tierra? ¿Cuál de los dos sistemas utiliza? Este postulado explica que, use el sistema que use, las leyes físicas siguen siendo las mismas; el Universo sigue siendo el mismo encuentre donde se encuentre.
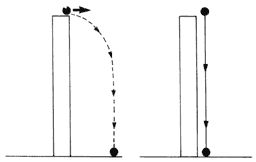
Siguiendo con el ejemplo del barco. Imagine que la piedra cae del mástil del barco. Si está quieto, la piedra caerá en línea recta, o se desviará ligeramente por la acción del viento.
Pero, ¿qué pasaría si el barco se moviese? Aquí entra lo esencial de la Relatividad. Si el barco tiene un movimiento y una velocidad constantes, si usted se encontrase en el interior del barco diría que la piedra cae en línea recta al mástil. Pero si usted estuviera en una orilla cercana, diría que se desviaría por el viento y que caería en el mástil por el movimiento del barco. Ahora bien, ¿cuál de las dos posturas es la correcta?
La Relatividad arguye que ambas son correctas, pues cada una usa un sistema de referencia distinto. Esto implica que todos los observadores tienen la misma autoridad y la misma razón al expresar sus opiniones, lo que implica que nada es absoluto, ni el tiempo, ni el espacio, ni nada. Esto chocaba con la opinión general de su época, que pensaba que el tiempo era algo absoluto. Einstein lo cambia y elimina la posibilidad de lo absoluto,
Aún así, no todo es relativo. Según la Relatividad, existe una única magnitud que es la misma en todos los sistemas: la velocidad de la luz. Einstein explica que la luz viaja en el vacío, contrariamente a la idea de la época de que la luz viajaba a través del éter.
 |
| La luz siempre viaja a la misma velocidad, independientemente de que haya movimiento o no |
Esto parece algo contrario a la lógica, pues podría parecer que se produce la misma situación que en el barco: cada uno de los observadores debería tener una visión personal de la velocidad de la luz. Pero Einstein afirma que, independientemente de los observadores, la luz siempre viaja a la misma velocidad.
Una de las consecuencias de este postulado es la dilatación del tiempo. Para ello, pongamos otro ejemplo. Imagine que usted se encuentra con su amigo Juan en el vacío del espacio, y se mueven a velocidad constante uno respecto al otro. Imagine que Juan lleva un reloj que funciona así: tiene dos espejos paralelos y entre ellos se encuentra un rayo de luz que rebota en cada uno de ellos. Cada rebote es un "tic" del reloj. Desde el punto de vista de Juan, al ser la velocidad de la luz fija, los "tics" siempre son constantes, pues la luz tarda lo mismo en ir de un espejo al otro.
 |
| El tiempo es fijo para Juan. |
Pero desde su punto de vista Juan se está moviendo. Por lo tanto, usted ve que el rayo de luz debe recorrer más distancia, pues debe sumar lo recorrido por Juan. Entonces, para usted el rayo de luz tarda más tiempo en hacer "tic". Y como la velocidad de la luz siempre es constante, la conclusión es que el tiempo se dilata, es decir, transcurre más despacio. Desde su punto de vista, cuanto más se aleje Juan, más despacio transcurre el tiempo para él.
 |
| El tiempo transcurre más despacio para usted. |
De este ejemplo también podemos sacar otra de las consecuencias: la contracción de la longitud. En este mismo ejemplo, si los dos medís lo que tarda la luz en llegar al espejo, Juan medirá, por ejemplo, un segundo, y usted que tarda dos. ¿Cómo es ésto? Según Juan, la luz se "acerca" a él, por lo tanto él medirá menos tiempo al medir lo que tarda la luz. La consecuencia de esto, como la luz siempre viaja a velocidad constante, es que el espacio se acorta para Juan. Por lo tanto, el tiempo se dilata y el espacio se contrae.
Otra de las consecuencias es la Relatividad de la Simultaneidad. Esto quiere decir que es imposible demostrar que dos sucesos ocurren al mismo tiempo, por lo tanto, no existe la simultaneidad. Pongamos otro ejemplo. Imagine que Juan está en el interior del vagón de un tren en movimiento. Usted se encuentra en la estación donde el tren pasa. Justo cuando el vagón pasa enfrente de usted, Juan enciende una bombilla en el centro del vagón. Desde el punto de vista de Juan, la luz llega a los dos extremos al mismo tiempo, de manera simultánea.
 |
| La luz llega en el mismo instante a ambos extremos. |
Pero, desde su punto de vista, el tren está en movimiento. Por lo tanto, usted ve que la luz llega antes al extremo contrario de la dirección del tren. Entonces ya no son sucesos simultáneos. Como es imposible demostrar que sólo uno tiene razón, la Relatividad explica que los sucesos simultáneos, simplemente, no existen.
 |
| La luz llega antes a uno de los extremos. |
Otra consecuencia es la equivalencia masa-energía. Según Einstein, cuanta más energía se aplica a un objeto, más aumenta su masa. Pongamos un ejemplo. Si usted comienza a empujar una bola de bolos cada vez más rápido, necesitará ir aplicando más y más fuerza conforme pasa el tiempo. Para explicar esto, la Relatividad dice que la masa aumenta conforme aumenta su energía. Al aumentar la velocidad del empuje, aumenta la energía de la bola de bolos; por lo tanto, aumenta su masa, y eso provoca que cada vez le cueste más empujarla.
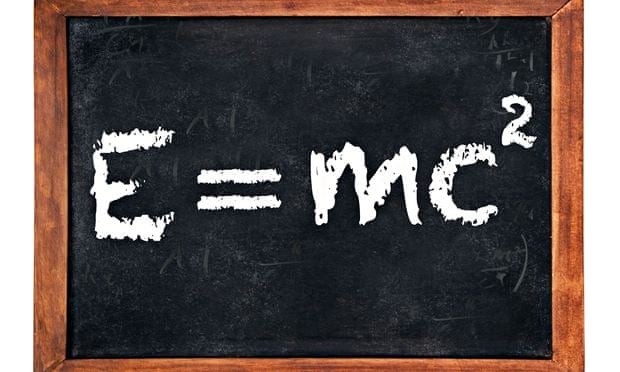 |
| La equivalencia masa-energía, seguramente la fórmula más famosa de la historia. |
Y la última consecuencia es la adición de velocidades. Pongamos un ejemplo. Usted y Juan se encuentran de nuevo en el espacio, alejándose uno del otro. Imagine que Juan le manda señales con una linterna a cada minuto. Usted verá que cada señal le llega más tarde, pues la luz recorre más distancia que en la señal anterior. Y justo lo contrario pasaría si se estuviesen acercando: que cada vez vería las señales en menos intervalo de tiempo.
Esta teoría cambió por completo el pensamiento de la época, pero eran contrarias a la Ley de la Gravitación Universal de Newton. Esto llevó a Einstein a formular la que sería una de las dos grandes teorías del siglo XX: la Relatividad General.







.jpg)





.jpg)













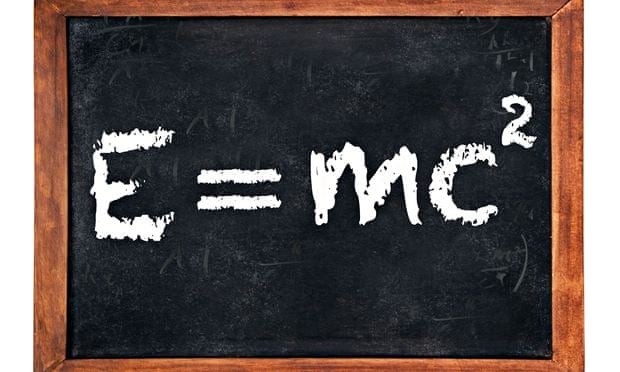




.jpg)